the proper way is to group it as 1+(-2)+3

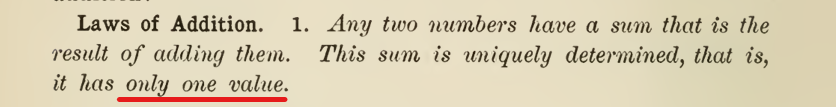
No it isn’t.

you can do it in any order

You can do it in any order anyway

left to right 1-2+3=-1+3=2

addition first 1+3-2=4-2=2

subtraction first -2+1+3=-1+3=2

right to left 3-2+1=1+1=2

What I meant with ““rule”” is the meme questions pray on people not understanding/remembering what the actual rules are

And you showed that you were one of them. Every answer you got other than 4 was wrong, because you didn’t understand the rules. spoiler alert: doing it in different orders never means add brackets to it. Addition first for 10-1+1 is 10+1-1, not 10-(1+1). See previous textbook example

why “left to right” conventions exist

They exist because people like you make mistakes when you try to do it in a different order. Either learn how the rules work or stop spreading disinformation. Well, you should stop spreading disinformation regardless.

I fully agree that if it comes down to “left to right”

It never does

But I’ve just shown why that “rule” is a common part

No you didn’t. You showed you didn’t understand the rules. Doing addition first for 10-1+1 is 10+1-1, not 10-(1+1). It literally means add all positive numbers together first, which are +10 and +1, as per Maths textbooks…

Note in the above simplification of the coefficients we have 6-11+5-7+2=6+5+2-11-7=13-18=-5, and not, as you claim 6-(11+5)-(7+2)=6-16-9=-19

because it is so weird and quite esoteric

It’s a convention, not a rule, and as such can be completely ignored by those who understand the rules. See literal textbook example

Maandelykse Mathematische Liefbebbery, Purmerende (1754-69)

You know the Facebook post is in English and from 2025, right? 😂

At least that’s not how I’ve been taught in school

If you had a bad teacher that doesn’t mean everyone else had a bad teacher.

You’re not teaching kids how to prove the quadratic formula, do you?

We teach them how to do proofs, including several specific ones.

No, you teach them how to use it instead.

We teach them how to use everything, and how to do proofs as well. Your whole argument is just one big strawman.

Again, with the order of operations

Happens to be the topic of the post.

It’s not a thing

Yes it is! 😂

I’ve given you two examples that don’t follow any

So you could not do the brackets first and still get the right answer? Nope!

2×2×(2-2)/2=0

2×2×2-2/2=7

That’s kinda random, but sure?

Not random at all, given you were talking about students understanding how Maths works.

2+3×4 then it’s not an order of operation that plays the role here

Yes it is! 😂 If I have 1 2-litre bottle of milk, and 4 3-litre bottles of milk, there’s only 1 correct answer for how many litres of milk of have, and it ain’t 20! 😂 Even elementary school kids know how to work it out just by counting up.

They all derive from each other

No they don’t. The proof of order of operations has got nothing to do with any of the properties you mentioned.

For example, commutation is used to prove identity

And neither is used to prove the order of operations.

2 operators, no order followed

Again with a cherry-picked example that only includes operators of the same precedence.

You have no property that would allow for (2+3)×4 to be equal 2+3×4

And yet we have a proof of why 14 is the only correct answer to 2+3x4, why you have to do the multiplication first.

Is that not correct?

Of course it is. So what?

It literally has subtraction and distribution

No it didn’t. It had Brackets (with subtraction inside) and Multiplication and Division.

I thought you taught math, no?

Yep, and I just pointed out that what you just said is wrong. 2-2(1+2) has Subtraction and Distribution.

2-2 is 2 being, hear me out, subtracted from 2

Which was done first because you had it inside Brackets, therefore not done in the Subtraction step in order of operations, but the Brackets step.

Also, can you explain how is that cherry-picking?

You already know - you know which operations to pick to make it look like there’s no such thing as order of operations. If I tell you to look up at the sky at midnight and say “look - there’s no such thing as the sun”, that doesn’t mean there’s no such thing as the sun.

You teach how to solve equations, but not the fundamentals

Nope. We teach the fundamentals. Adults not remembering them doesn’t mean they weren’t taught. Just pick up a Maths textbook. It’s all in there. Always has been.

Fundamentals, most of the time, are taught in universities

No they’re not. They only teach order of operations from a remedial point of view. Most of them forget about The Distributive Law. I’ve seen multiple Professors be told by their students that they were wrong.

it’s not really math in a sense that you don’t understand the underlying principles

The Constructivist learners have no trouble at all understanding it.

Nope.

Yep!

There’s only commutation, association, distribution, and identity.

And many proofs of other rules, which you’ve decided to omit mentioning.

It doesn’t matter in which order you apply any of those properties, the result will stay correct

But the order you apply the operations does matter, hence the proven rules to be followed.

2×2×(2-2)/2

Notably you picked an example that has no addition, subtraction, or distribution in it. That’s called cherry-picking.

Completely different order, yet still correct

Yep, because you cherry-picked a simple example where it doesn’t matter. It’s never going to matter when you only pick operations which have the same precedence.

My response to the rest goes back to the aforementioned

…cherry-picking.

No, I am saying you are wrong

And textbooks, calculators, accountants, and @sxan@midwest.social, who also explicitly pointed out that what you did was 10-(1+1). I see you didn’t read the textbook either then.

No one else

Nope, also all the other parties listed above, who all agree with me

The saddest, and funniest, part is that you are so egotistical that you don’t see why you are wrong

That would be you again, after it has been explained to you many times, by me, other commentators, and Maths textbooks.

Maybe you will get it one day, but I won’t be there for it

Again that applies to you only, the only one here who thinks 10-1+1=8 when doing addition first, even though 11-1=10.

Self reflection is good.

How do you know when you haven’t tried it yet? If you had, you would realise you also owe @cabron_offsets@lemmy.world an apology too

I know it is wrong, which is why I am telling you what my mistake was originally

But failing to understand what your actual mistake was, coming up with -1+1=-2, and not -1+1=-0

The fact that you still don’t get it demonstrates your complete lack of understanding

That would be you, the one who thinks order matters, and that -1+1=-2, not -0.

Order does matter

Nope!

+10-1+1=10

+10+1-1=10

-1+10+1=10

+1+10-1=10

+1-1+10=10

-1+1+10=10

Put those all into a calculator, and/or ask an accountant about it.

that order is left to right.

And yet, going RIGHT TO LEFT +1-1+10=0+10=10, same answer… though I have no doubt you think it’s +1-1+10=+1-11=-10

The original equation is written correctly

and 10-(1+1) isn’t, hence your continued wrong answer

My mistake was doing the addition before the subtraction when the equation reads 10 - 1 + 1

No, your mistake was doing 10-(1+1) where the question reads 10-1+1, and not +10+1-1 <== this is addition first, you add all the positive numbers together first, then do the negative numbers This is literally the textbook way to do it

According to you 6a²b-11a²b+5a²b-7a²b+2a²b=6a²b-16a²b-9a²b=-19a²b, and yet the textbook quite clearly states it’s -5a²b, which is because it’s 6a²b+5a²b+2a²b-11a²b-7a²b=13a²b-18a²b, and NOT 6a²b-(11a²b+5a²b)-(7a²b+2a²b)

10-(1+1)=10-1-1 which is what you did, which is not 10-1+1. You “added” 1 to -1, and got -2 instead of 0

How are you still not getting this?

It’s not me who’s not getting it.

No it wasn’t.

Yes it was. Read the textbooks.

The original equation is written correctly but the logic is incorrect

No your logic is incorrect. You’re incorrectly adding brackets to it.

in order to make it work the way I declared you have to do the equation x - y + z doing the y + z first

By putting it in brackets which is not how addition is done first. Doing addition first for x - y + z is x + z - y, not x - (y + z)

which was the mistake doing addition then subtraction

No, the mistake was you put the addition in brackets, -(1+1)=-2, not -1+1=+1-1=0. As per the textbook, the sum of any 2 numbers can only have 1 value. That 1 value for -1 and +1 is 0. -1+1=0, +1-1=0, not -1+1=-2

doing addition then subtraction instead of addition and subtraction in order from left to right

The rules are you either do addition then subtraction, OR you do left to right. There is no such thing as addition then subtraction left to right.

Addition then subtraction 10+1-1=11-1=10

Left to right 10-1+1=9+1=10

What you did 10-(1+1)=10-2=8

I see you are still being a bad teacher

says bad student, who didn’t try what the teacher said to try

who refuses to listen

that would be you again. You didn’t try it on a calculator, you didn’t ask an accountant. You didn’t even read and understand my examples. Read the textbook - it’s not just me telling you this.

I am not continuing with you

Because you’re unwilling to admit you’re wrong and refuse to try what the teacher and textbook have told you to do, and also refuse to ask an accountant about it

The fact that you still don’t get it demonstrates bad faith

Nope, that’s you again. You’re even arguing with literal textbook examples.

willful ignorance, and an unwarranted superiority complex

Also you, thinking you’re above Maths teachers, calculators, accountants, and Maths textbooks. According to you all of us are wrong, and only you are right. Get a grip

Welcome to the 21st century

Welcome to it’s not a textbook (and it wasn’t about order of operations anyway).

We have this thing called the internet so people can share information without killing trees

We also have this thing called textbooks, that schools order so that Maths classes don’t have to be held in computer labs.

It’s the resource material for a college course

And the college doesn’t teach order of operations.

That’s like the definition of a text book

by someone who can’t back up their statements with actual textbooks.

One is a PhD teaching a college course on the subject

Yep, exactly what I said - a random person as far as order of operations is concerned, since he teaches Set Theory and not order of operations.

the other is Wolfram

Yeah, their programmers didn’t know The Distributive Law either.

I’m willing to bet their credentials beat “claims to be a high school math teacher” pretty soundly

Happy to take that bet. Guarantee you neither of them has studied order of operations since they were in high school.

This portion of the discussion wasn’t about order of operations

Yes it is. I said that order of operations dictates that you have to solve binary operators before unary operators, then you started trying to argue about unary operators.

it was about the number of inputs an operator (+, and - in this case) has

Yep, the ones with more inputs, binary operators, have to be solved first.

Try to keep up

Says person who’s forgotten why we were talking about it to begin with! 😂

At least your repeated use of the plural maths means you’re not anywhere near my kids.

Well that outs yourself as living in a country which has fallen behind the rest of the world in Maths, where high school teachers don’t even have to have Maths qualifications to teach Maths.

when those symbols are being used as a “sign of the quality” of the number it’s referring to

which is always. As usual, the comprehension issue is at your end.

not when it’s being used to indicate an operation like addition or subtraction

Yes it is 😂

Hopefully that clears it up

That you still have comprehension issues? I knew that already

This is ignoring the fact that a random screen shot could be anything

The name of the book is in the top left. Not very observant either.

For all I know you wrote that yourself

You don’t care how much you embarrass yourself do you, given the name of the book is in the top left and anyone can find and download it. 😂

because the first “+” isn’t an operator

Yes it is! 😂

It’s, as your own picture says, a sign of the quality of 2

and a sign of the quality of the 3 too. There are 2 of them, one for each Term, since it’s a 1:1 relationship.

I would love to know how you get to a sum or difference with only one input.

You don’t. Both need 2 Terms with signs. In this case +2 and +3.

2 is the first, and 3 is the second

Yep, corresponding to the 2 plus signs, +2 and +3. 1 unary operator, 1 Term, 2 of each.

Two inputs for addition

2 jumps on the number line, starting from 0, +2, then +3, ends up at +5 on the number line. This is how it’s taught in elementary school.

Did you get it this time?

The real question is did you?

Was that too fast?

No, you just forgot one of the plus signs in your counting, the one we usually omit by convention if at the start of the expression (whereas we never omit a minus sign if it’s at the start of the expression).

You can go back and read it again if you need to

I’m not the one who doesn’t know how unary operators work. Try it again, this time not leaving out the first plus sign.

Fine, operation then

Nope, not an operation either.

The fact that you think “!” is the same thing as brackets

I see you don’t know how grouping symbols work either.

Maybe you’re just being weirdly pedantic about operator vs operation

Grouping symbols are neither.

Which would be a strange hill to die on since the original topic was operations

You were the one who incorrectly brought grouping symbols into it, not me.

I could keep providing sources

You haven’t provided any yet! 😂

I still don’t have the time to screen shot some random crap with no supporting evidence

Glad you finally admitted you have no supporting evidence. Bye then! 😂

10-1+1=10 only if you don’t the addition first 1 + 1 = 2 - 10 = 8

Nope, yet again you just did 10-(1+1), which is wrong for 10+1-1. It gives 10 in any order. 10+1-1=11-1=10 <== did addition first, got 10. Accountants would have a nightmare if order mattered. “Did we receive this payment first, or this invoice? The order matters! ARGH!”

which was my mistake, which I already stated.

No, your mistake was adding brackets, 10-(1+1) ISN’T how to do addition first. 10+1-1 is. Ask an accountant! 😂 As you discovered 10-(1+1)=10-1-1, which isn’t 10+1-1, nor 10-1+1. 10-1-1=8, which is what you did - 10-1-1=10-(1+1) - 10-1+1=10, 10+1-1=10.

I see you still didn’t try it on a calculator yet then

Enjoy the egg on your face bud

None on my face. My students do very well in their tests. How about you? BTW try it on a calculator and guess what answer you’ll get. hint: it’ll be the same answer regardless of which order you do it 😂

To save you some trouble, here’s the results from my calculator…

10+1-1=10

10-1+1=10

-1+10+1=10

+1+10-1=10

-1+1+10=10

1-1+10=10

It is though. Here’s a link to buy a printed copy:

BWAHAHAHAHAHAHA! They print it out when someone places an order! 😂

You keep mentioning textbooks but haven’t actually shown any that support you. I have

No you haven’t. You’ve shown 2 websites, both updated by random people.

I’ll trust the PhD teaching a university course on the subject

I already pointed out to you that they DON’T teach order of operations at University. It’s taught in high school. Dude on page you referred to was teaching Set theory, not order of operations.

over the nobody on the internet

Don’t know who you’re referring to. I’m a high school Maths teacher, hence the dozens of textbooks on the topic.

Talking about yourself in the third person is weird

Proves I’m not weird then doesn’t it.

Even your nonsense about a silent “+”

You call what’s in textbooks nonsense? That explains a lot! 😂

is really just leaving off the leading 0 in the equation 0+2

And yet the textbook says nothing of the kind. If I had 2+3, which is really +2+3 (see above textbook), do I, according to you, have to write 0+2+0+3? Enquiring minds want to know. And do I have to put another plus in front of the zero, as per the textbook, +0+2+0+3

Because addition is a binary operator

No it isn’t 😂

Only the ones that operate on two inputs.

Now you’re getting it. Multiply and divide take 2 inputs, add and subtract take 1.

Some examples of unary operators are factorial, absolute value, and trig functions.

Actually none of those are operators. The first 2 are grouping symbols (like brackets, exponents, and vinculums), the last is a function (it was right there in the name). The only unary operators are plus and minus.

I can’t keep trying to explain the same thing to you

You very nearly got it that time though! 😂

at least less wrong

Again, it’s not me who’s wrong.

I feel bad for your students if you cannot see why you are wrong here

My students know I’m right. Everyone’s students know that’s right. It’s only adults who’ve forgotten the rules who get this wrong.

The “mysterious” they is HerelAm, the person I was replying to you ninny

The person who couldn’t even manage to get 10-1+1 correct when doing addition first 😂

No worries :-)

THEY took the position we should have brackets defining the order in every single equation or otherwise have them as undefined TODAY

Who’s this mysterious “THEY” you are referring to, because I can assure you that the history of Maths tells you that is wrong. e.g. look in Cajori and you’ll find the order of operations rules are at least 2 centuries older than the use of Brackets in Maths.,

It doesn’t matter when they were invented

The rules haven’t changed since then.

They are the one arguing it SHOULD BE

…and watch Physicists and Mathematicians promptly run out of room on blackboards if they did.

You’re getting caught up in the semantics of the wording

No, you’re making up things that never happened.

they’re saying brackets were always around and we chose left to right to avoid bracket mess

and that’s wrong. Left to right was around before Brackets were.

we chose and continue to choose to keep using the left to right convention over brackets everywhere

and you’re wrong, because that choice was made before we’d even started using Brackets in Maths, by at least a couple of centuries.

it would be unnecessary and make things more cluttered

They’ve always been un-necessary, unless you want to deviate from the normal order of operations.

They could have decided we should use them in every equation for absolute clarity of order

But they didn’t, because we already had clarity over order, and had done for several centuries.

Saying we should not do that based on tradition alone is a bad reason.

Got nothing to do with tradition. Got no idea where you got that idea from.

Things DO change.

The order of operations rules don’t, and the last change to the notation was in the 19th Century.

I could go on

and you’d still be wrong. You’re heading off into completely unrelated topics now.

you should argue more than “it’s tradition” or “we’ve done fine without it so far”

I never said either of those things.

Because they did fine with many things in mathematics until they decided they needed to change or expand it

And they changed the meaning of the Division symbol sometime in the 19th Century or earlier, and everything has been settled for centuries now.

Actually, it is. Written by a PhD and used in a college course.

Yeah there’s an issue with them having forgotten the basic rules, since they don’t actually teach them (except in a remedial way). Why do you think I keep trying to bring you back to actual Maths textbooks?

May want to work on your own reading comprehension.

Nope. It’s still not a textbook. Sounds more like a higher education version of Wikipedia.

The facts disagree

With you, yes.

it doesn’t change the underlying issue that it’s defined by man.

The notation is, the rules aren’t.

In the absence of all your books (which you clearly don’t understand anyway based on our discussion of unary vs binary)

Says person who doesn’t understand the difference between unary and binary. Apparently EVERYTHING is binary according to you (and your website). 😂

order of operations only exists because we all agree to it

It exists whether we agree with it or not. Don’t obey it, get wrong answers.

What proof do you have that using a left to right rule is universally true?

From my understanding It’s an agreed convention that is followed

Read what I wrote again. I already said that left to right is a convention, and that Left Associativity is a rule. As long as you obey the rule - Left Associativity - you can follow whatever convention you want (but we teach students to do left to right, because they often make mistakes with signs when they try doing it in a different order, as have several people in this thread).

that implies we could have a right to left rule

You can have a right to left convention if the rule is Right Associativity.

It’s also true that not all cultures right in the same way

Yeah, I don’t know how they do Maths - if they do it the same as us or if they just flip everything back-to-front (or top to bottom - I guess they would). In either case all the rules on top stay the same once the direction is established (like I guess exponents would now be to the top left not the top right? but in any case the evaluation of an exponent would stay the same).

But here is an interesting quote from Florian Cajori in his book a history of mathematical notations

Yeah, he’s referring to the conventions - such as left to right - not the rule of Left Associativity, which all the conventions must obey. For a while Lennes was doing something different - because he didn’t understand Terms - and was disobeying Left Associativity, (which meant his rules were at odds with everyone else), but his rule died out within a generation of his death,. Absolutely all textbooks now obey Left Associativity, same as before Lennes came along.

Lastly here is an article that also highlights the issue

Not really. Just another person who has forgotten the rules.

“as it happens, the accepted convention says the second one is correct”

No it isn’t. The Distributive Law says the first is correct (amongst 4 other rules of Maths which also say the answer is only 1). The second way they did it disobeys The Distributive Law (and 4 other rules) and is absolutely wrong.

That better?

Is it a Maths textbook?

Or you can find one you like all by yourself

I already have dozens of Maths textbooks thanks.

And you can shove the condescension up your ass until you understand the difference between unary and binary operators

It’s not me who doesn’t understand the difference.

you’re proving my point for me.

Still need to work on your comprehension then. I did nothing of the sort.

There is no fundamental law of the universe that says multiplication comes first.

Yes there is. The fact that it’s defined as repeated addition. You don’t do it first, you get wrong answers.

It’s defined by man and agreed to

It’s been defined and man has no choice but to agree with the consequences of the definition, or you get wrong answers.

But they could very well prioritize addition and subtraction over multiplication and division

No they couldn’t. It gives wrong answers.

I said it’s a mistake to think one of them has a precedence over the other

And I said it’s not a mistake. You still get the right answer.

You’re arguing the same point I’m making?

No, I’m telling you that prioritising either isn’t a mistake. Mistakes give wrong answers. Prioritising either doesn’t give wrong answers.

Very confidently getting basic facts wrong doesn’t inspire confidence in the rest of your comments.

…says person quoting Wikipedia and NOT a Maths textbook! 😂

Your example still doesn’t give a reason why 2 + 3 * 4 is 2 + 3 + 3 + 3 +3

Yes it does., need to work on your comprehension…

Multiplication is defined as repeated addition - 3x4=3+3+3+3

other than that we all agree to it

You can disagree as much as you want and 3x4 will still be defined as 3+3+3+3. It’s been that way ever since Multiplication was invented.